

Este é um evento online
Conhecendo um pouco mais sobre a Geometria Espacial.
?Visando contribuir com os Licenciados em
Matemática da UEMG-Unidade Carangola, buscamos com esse projeto contribuir com
a formação acadêmica dos futuros educadores contribuir com a possibilidade da
inclusão do GeoGebra como recurso tecnológico para auxílio no processo de
ensino aprendizagem com enfoque na Geometria Espacial: Poliedros.
E afinal, o que são poliedros?
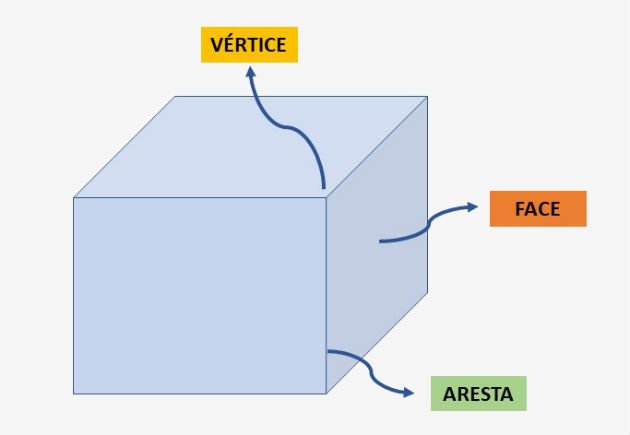
Os poliedros são sólidos geométricos limitados por um número finito de polígonos planos. Esses polígonos formam as faces do poliedro.
A intersecção de duas faces é chamada de aresta e o ponto comum de três ou mais arestas é chamado de vértice, conforme indicado na imagem abaixo.
Os poliedros podem ser convexos ou não convexos. Se qualquer segmento de reta que liga dois pontos de um poliedro estiver totalmente contido nele, então ele será convexo.
Uma outra forma de identificar um poliedro convexo é verificar que qualquer reta não contida em nenhuma das face e nem paralela a elas, corta os planos das faces em, no máximo, dois pontos.

Onde,
F: número de faces
V: número de vértices
A: número de arestas
Os poliedros em que a relação de Euler é válida são chamados de eulerianos. É importante notar que todo poliedro convexo é euleriano, porém nem todo poliedro euleriano é convexo.
GeoGebra e os poliedros: um recurso a ser explorando.
Com esse trabalho, espera-se que os alunos possam atuar como inovadores, levando para dentro da sala de aula, uma oportunidade de tornar o ensino mais significado e dinâmico para os alunos. Muitas vezes, eles não conseguem aprender por falta de motivação, o conteúdo não é ministrado de uma forma a deixá-lo mais intrigante e desafiador. Com isso, os professores podem realizar uma metodologia que busca ressaltar o lúdico juntamente com as novas tecnologias como ferramenta metodologia de ensino para os Poliedros.
UM OUTRO OLHAR: OUTRAS MANEIRAS DE TRABALHAR COM POLIEDROS
{{'Label_DoacaoAPartir' | translate}} {{item.valores[0].valor | currency:viewModel.evento.moeda}}
{{item.descricao}}{{entrada.valorComDesconto | currency:viewModel.evento.moeda}}
